Las esferas geodésicas son superficies poliédricas adecuadas a esferas. Se pueden construir partiendo de un poliedro regular en el que se triangulan sus caras. Cada nueva triangulación del nuevo vértice que obtenemos, debe estar inscrito en la esfera, generando la superficie más homogénea posible, aunque esto a veces no sea posible teniendo que producir superficies cuyos triángulos no siempre son todos equiláteros.
Las esferas geodésicas son superficies poliédricas adecuadas a esferas. Se pueden construir partiendo de un poliedro regular en el que se triangulan sus caras. Cada nueva triangulación del nuevo vértice que obtenemos, debe estar inscrito en la esfera, generando la superficie más homogénea posible, aunque esto a veces no sea posible teniendo que producir superficies cuyos triángulos no siempre son todos equiláteros.
En la figura observamos cómo se puede transformar un poliedro arquimediano (icosaedro truncado) en una esfera geodésica, esto es, en una estructura construida con caras triangulares casi equiláteras, de manera que todos los vértices de los triángulos de la esfera equidistan del centro de la misma. Sobre cada una de las caras de la figura se construye una pirámide cuya base es la misma cara. Para saber cuál es su altura debemos pasar por el punto medio de la cara una recta que pase también por el centro de la esfera que inscribe el poliedro. Esta recta cortará a la esfera en la que está inscrito el poliedro en un punto y este es el vértice superior de la pirámide. A continuación unimos este vértice con cada uno de los vértices de la base que son los vértices del polígono regular (caras del poliedro arquimediano). De esta forma tenemos que todos los puntos de la esfera geodésica equidistan del centro y todas sus caras son triángulos casi equiláteros.
Geodésica hexaédrica de frecuencia 2
Partimos de un cubo y marcamos los vértices que aparecen en el hemisferio de la parte derecha en círculos naranjas. Luego proyectamos las aristas del cubo sobre la esfera y dividimos cada una en dos partes, eso significa que cada cuadrado tendrá su diagonal dividida en otras partes, de esta forma la cara proyectada se transforma en una pirámide de 4 lados en color amarillo y es la que corresponde a la proyección del centro de la cara y luego una consecución de triángulos alternos entre el color azul, magenta y verde.
Hemisferio g. icosaédrico de frecuencia 4
En este caso dividimos la arista en cuatro partes y proyectamos esa división sobre la esfera, de esta manera salen los 16 triángulos esféricos sobre lo que correspondería a cada cara del icosaedro.
Geodésica hemisférica icosaédrica de frecuencia 4
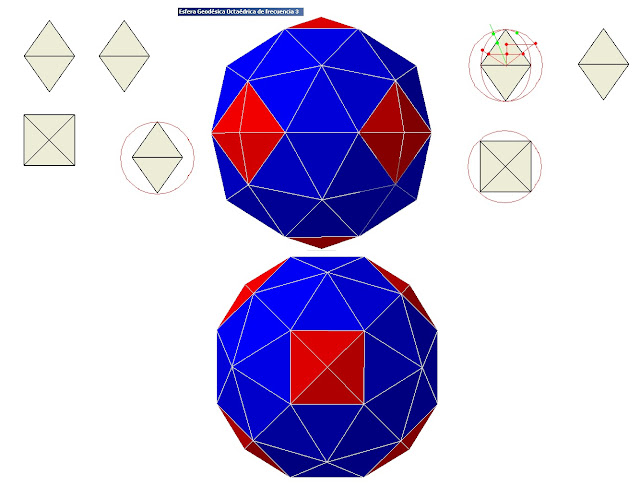
Geodésica octaédrica de frecuencia 6
---------------------
---------------------
Esferas geodésicas:
Esfera geodésica hexaédrica de frecuencia 1
Esfera geodésica hexaédrica de frecuencia 2
Esfera geodésica octaédrica de frecuencia 2
Esfera geodésica octaédrica de frecuencia 3
Esfera geodésica octaédrica de frecuencia 3 con proyecciones diédricas iguales
Esfera geodésica octaédrica de frecuencia 4.
Esfera geodésica dodecaédrica de frecuencia 1
Esfera geodésica dodecaédrica de frecuencia 2
Esfera geodésica icosaédrica de frecuencia 2
Esfera geodésica icosaédrica de frecuencia 3
Esfera geodésica icosaédrica de frecuencia 4
Geodésica dodecaédrica de frecuencia 2
Geodésica icosaédrica de frecuencia 2 o de icosidodecaedro
Geodésica icosaédrica de frecuencia 6
Geodésica octaédrica de frecuencia 2
Geodésica octaédrica de frecuencia 3
Geodésica dodecaédrica de frecuencia 1
Geodésica octaédrica de frecuencia 3
Geodésica octaédrica de frecuencia 6
Geodésica icosaédrica de frecuencia 2
Geodésica icosaédrica de frecuencia 2
Geodésica icosaédrica de frecuencia 2 con su disposición respecto al icosaedro
Geodésica icosaédrica de frecuencia 3
---------------------------------------------------------------------
Geodésica dodecaédrica de frecuencia 2
------------------------------------------------------------------------------------------------------
Geodésicas a partir del cubo
Geodésica hexaédrica de frecuencia 3
Geodésica hexaédrica de frecuencia 1
Geodésica icosaédrica de frecuencia 2
Geodésica octaédrica de frecuencia 4

Geodésica cuboctaédrica de frecuencia 3

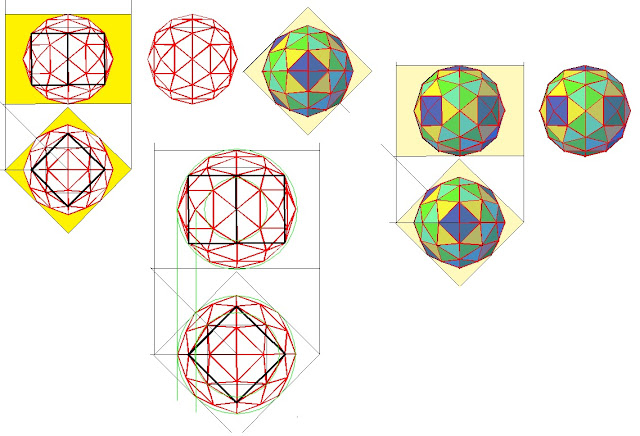
Geodésicas en sistema diédrico
 Geodésica dodecaédrica de frecuencia 1
Geodésica dodecaédrica de frecuencia 1
Geodésica dodecaédrica de frecuencia 2
Geodésica icosaédrica de frecuencia 2
Geodésica icosaédrica de frecuencia 3
Semiesfera Geodésica icosaédrica de frecuencia 2
Semiesfera Geodésica hexaédrica de frecuencia 2
Geodésica octaédrica de frecuencia 3